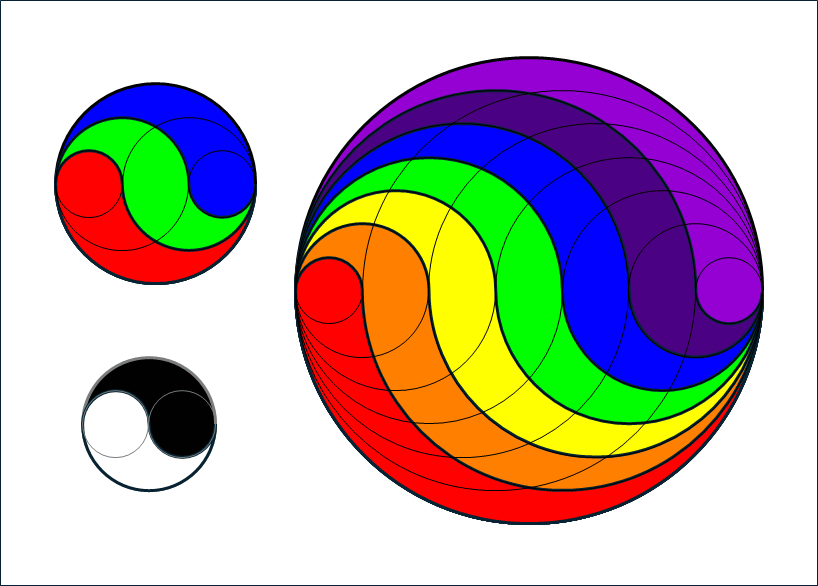One inspiration I got from Bosman's book is "generalized Yin Yang".
-
One inspiration I got from Bosman's book is "generalized Yin Yang". You can subdivide the circle into parts that have both equal area and equal circumference. The lines defining the subdivisions are all circle segments with integer relative diameters.
The Yin Yang is a powerful symbol. The rainbow is also often used these days to symbolize diversity. I was quite pleased with the possibility of combining these 2 symbols. -
One inspiration I got from Bosman's book is "generalized Yin Yang". You can subdivide the circle into parts that have both equal area and equal circumference. The lines defining the subdivisions are all circle segments with integer relative diameters.
The Yin Yang is a powerful symbol. The rainbow is also often used these days to symbolize diversity. I was quite pleased with the possibility of combining these 2 symbols.@GerardWestendorp in the usual yin-yang symbol there's also a spot of yan in the ying and vice versa. With an order-7 version of the same thing I suppose you'd want a spot of _every_ colour in every other colour.
(If nothing else, if you want to use it as a symbol of diversity, the idea that "there's always a little bit of $this_category in $that_category" seems likely to raise the blood pressure of anti-diversity people, which is surely a feature rather than a bug.)
In the order-2 symbol the natural place to put each opposite-coloured spot is to make it a small circle centred in the larger circle. I don't know if there's any particularly 'nice' layout for the spots in the order-7 symbol. Your construction lines divide each region into _seven_ parts, not six. Placing the spots might have to be done by art rather than mathematics.
But at least there's the extra resonance that the total number of spots would be 42.
-
@GerardWestendorp in the usual yin-yang symbol there's also a spot of yan in the ying and vice versa. With an order-7 version of the same thing I suppose you'd want a spot of _every_ colour in every other colour.
(If nothing else, if you want to use it as a symbol of diversity, the idea that "there's always a little bit of $this_category in $that_category" seems likely to raise the blood pressure of anti-diversity people, which is surely a feature rather than a bug.)
In the order-2 symbol the natural place to put each opposite-coloured spot is to make it a small circle centred in the larger circle. I don't know if there's any particularly 'nice' layout for the spots in the order-7 symbol. Your construction lines divide each region into _seven_ parts, not six. Placing the spots might have to be done by art rather than mathematics.
But at least there's the extra resonance that the total number of spots would be 42.
@simontatham
Hmm, don't know about the dots.
Maybe you could personalize them by putting faces on them. -
@simontatham
Hmm, don't know about the dots.
Maybe you could personalize them by putting faces on them.@GerardWestendorp @simontatham One way to include the other elements: use the symbol with one fewer elements. Here's three elements with two-element dots.
With seven elements, the dot could be the six-element symbol, but I've yet to find a good way to draw these.
-
@GerardWestendorp @simontatham One way to include the other elements: use the symbol with one fewer elements. Here's three elements with two-element dots.
With seven elements, the dot could be the six-element symbol, but I've yet to find a good way to draw these.
@foldworks What if we make it recursive, so the inner symbol has dots of its own?
@GerardWestendorp @simontatham -
@foldworks What if we make it recursive, so the inner symbol has dots of its own?
@GerardWestendorp @simontatham@anshthewad @GerardWestendorp @simontatham OK, here it is (this version uses minimal outlines)
-
@anshthewad @GerardWestendorp @simontatham OK, here it is (this version uses minimal outlines)
@foldworks @anshthewad @GerardWestendorp here's the recursive version of mine, although converting it into PNG for upload doesn't really do it justice. If only Mastodon let me keep it as SVG, you'd be able to confirm that the recursion continues for all 7 levels by zooming in!
-
@foldworks @anshthewad @GerardWestendorp here's the recursive version of mine, although converting it into PNG for upload doesn't really do it justice. If only Mastodon let me keep it as SVG, you'd be able to confirm that the recursion continues for all 7 levels by zooming in!
@simontatham @foldworks @anshthewad @GerardWestendorp And now I'm wondering how this would look like printed on a Standard Sticker (maybe it's too small, and it's definitely too small to see more than 3 levels of recursion, but still)